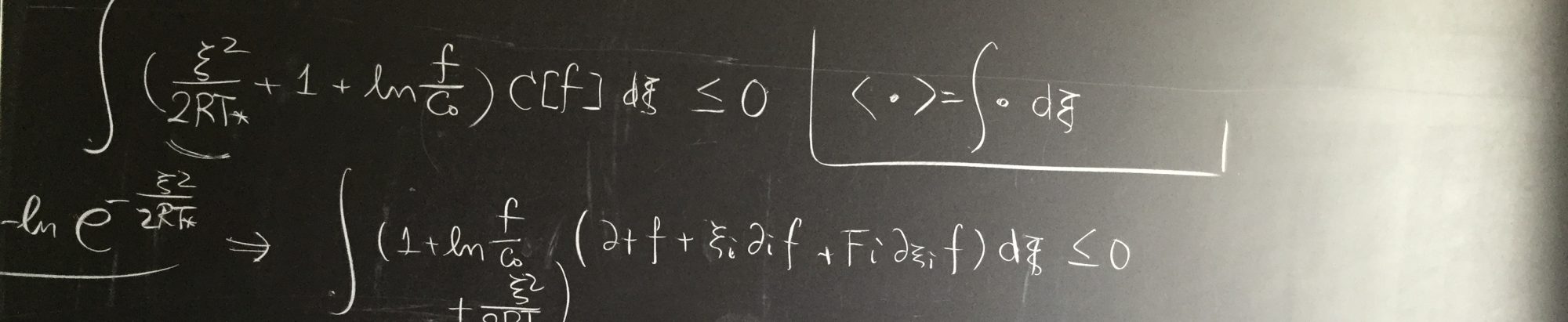Category Archives: 非平衡現象の流体力学

分科会「非平衡現象の流体力学」（第15回）

平成27年度第2回講演会（日本航空宇宙学会関西支部分科会）

日時： 平成27年4月24日（金）　16:30-17:30
場所： 京都大学 桂キャンパスCクラスタ総合研究棟III（C3棟）　3階　b3n03室（航空宇宙工学専攻会議室）
講演： From Vlasov-Poisson to Euler for trapped particles
Prof. Julien Barre
(Laboratoire J. A. Dieudonné, Université de Nice-Sophia Antipolis, France)
要旨： Motivated by experimental studies on clouds of cold atoms, we investigate the strong interaction limit (a.k.a. “quasi neutral” limit) for a Vlasov-Poisson-Fokker-Planck equation in an external potential. We show that under certain conditions, the dynamics reduces to an incompressible fluid equation: Euler or the lake equation, depending on the external potential. We will illustrate this convergence by some direct numerical simulations of the particles system.

分科会「非平衡現象の流体力学」（第14回）

平成27年度第1回講演会（日本航空宇宙学会関西支部分科会）

日時： 平成27年4月9日（木）　16:30-17:30
場所： 京都大学 桂キャンパスCクラスタ総合研究棟III（C3棟）　3階　b3n03室（航空宇宙工学専攻会議室）
講演： Sub-shock formation in gas mixtures
Prof. Fiammetta Conforto
(Dipartimento di Mathematica e Informatica, Universita degli Studi di Messina, Italy)
要旨：  Abstract

分科会「非平衡現象の流体力学」（第13回）

平成26年度第13回講演会（日本航空宇宙学会関西支部分科会）

日時： 平成27年2月9日（月）　14:40-15:40
場所： 京都大学 桂キャンパスCクラスタ総合研究棟III（C3棟）　3階　b3n03室（航空宇宙工学専攻会議室）
講演： Global Solutions of the Boltzmann Equation over R^D near Global Maxwellians with Small Mass
(joint work with Claude Bardos, Irene M. Gamba, and C. David Levermore)
Prof. François Golse
(Centre de mathématiques Laurent Schwartz, Ecole Polytechnique, France)
要旨：  We study the dynamics defined by the Boltzmann equation set in the Euclidean space R^D in the vicinity of global Maxwellians with finite mass. A global Maxwellian is a special solution of the Boltzmann equation for which the collision integral vanishes identically. In this setting, the dispersion due to the advection operator quenches the dissipative effect of the Boltzmann collision integral. As a result, the large time limit of solutions of the Boltzmann equation in this regime is given by noninteracting, freely transported states and can be described with the tools of scattering theory.

分科会「非平衡現象の流体力学」（第12回）

平成26年度第12回講演会（日本航空宇宙学会関西支部分科会）

日時： 平成27年1月13日（火）　14:40-16:20
場所： 京都大学 桂キャンパスCクラスタ総合研究棟III（C3棟）　3階　b3n03室（航空宇宙工学専攻会議室）
講演1：
(1 hour)		 From Stochastic Differential Games and Kinetic Theory Methods To the Modeling of Behavioral Social Crowds
Prof. Nicola Bellomo
(Department of Mathematical Sciences, Politecnico di Torino, Italy)
要旨1：  Abstract
講演2：
(30 min)		 A Monte Carlo simulation on the basis of the kinetic theory for chemo-tactic bacteria
Prof. Shugo Yasuda
(Graduate School of Simulation Studies, University of Hyogo, Japan)
要旨2：  Abstract

分科会「非平衡現象の流体力学」（第11回）

平成26年度第11回講演会（日本航空宇宙学会関西支部分科会）

日時： 平成27年1月6日（火）　16:10-17:10
場所： 京都大学 桂キャンパスCクラスタ総合研究棟III（C3棟）　3階　b3n03室（航空宇宙工学専攻会議室）
講演：
On Coagulation-Fragmentation Models with Spatial Diffusion
(joint work with Laurent Desvillettes, J. A. Canizo, J. A. Carrillo)
Prof. Klemens Fellner
(Institute for Mathematics and Scientific Computing, University of Graz, Austria)
要旨：
We consider existence, large-time behaviour and fast-reaction limits of coagulation-fragmentation models with spatial diffusion, which share many formal and structural  similarities with kinetic equations. As continuous-in-size model, we study Smoluchowski’s equation with constant coefficients and prove explicit convergence to equilibrium also in the case of degenerate diffusion coefficients.
Discrete-in-size models are considered with more general coefficients. The diffusion coefficients are also allowed to degenerate in size.
The main techniques include a-priori estimates based on the dissipation of an  entropy functional, entropy entropy-dissipation methods, moment bounds and  duality methods.

分科会「非平衡現象の流体力学」（第10回）

平成26年度第10回講演会（日本航空宇宙学会関西支部分科会）

日時： 平成26年12月11日（木）　16:30-17:30
場所： 京都大学 桂キャンパスCクラスタ総合研究棟III（C3棟）　3階　b3n03室（航空宇宙工学専攻会議室）
講演： A Hybrid Numerical Method for Multi-Scale Collisional Kinetic Equations
Dr. Thomas Rey
(Laboratoire Paul Painleve, Universite Lille 1, France)
要旨： In this work in collaboration with F. Filbet, we construct a hierarchy of hybrid numerical methods for multi-scale kinetic equations based on moment realizability matrices, a concept introduced by Levermore, Morokoff and Nadiga. Following such a criterion,  one can consider hybrid scheme where the hydrodynamic part is given either by the compressible Euler or Navier-Stokes equations, or even with more general models, such as the Burnett or super-Burnett systems.We present applications of this method to the Boltmann equation for rarefied gases, in one dimension of space and three dimensions of velocity, for both Euler and Navier-Stokes fluid description. We prove numerically that our hierarchy of hybrid fluid-kinetic solvers can provide different numerical methods able to achieve the accuracy of a pure kinetic one, with efficiency sometimes almost comparable with the one of a fluid model.

分科会「非平衡現象の流体力学」（第9回）

平成26年度第9回講演会（日本航空宇宙学会関西支部分科会）

日時： 平成26年12月1日（月）　14:40-15:40
場所： 京都大学 桂キャンパスCクラスタ総合研究棟III（C3棟）　3階　b3n03室（航空宇宙工学専攻会議室）
講演： Singularity of macroscopic variables near boundary for gases  with  cut-off  hard potential
Dr. I-Kun Chen
(Graduate School of Informatics, Kyoto University, Japan)
要旨： The boundary singularity for stationary solutions of the linearized Boltzmann equation with cut-off hard potential is analyzed. A technique of using the Holder type  continuity of the integral operator to obtain the integrability of the derivatives of  the macroscopic variables is developed. We establish the asymptotic approximation for the gradient of the moments. Our analysis indicates the logarithmic singularity of the gradient of the moments. In particular, our theorem holds for the condensation and evaporation problem.

分科会「非平衡現象の流体力学」（第8回）

平成26年度第8回講演会（日本航空宇宙学会関西支部分科会）

日時： 平成26年10月20日（月）　14:30-15:30
場所： 京都大学 桂キャンパスCクラスタ総合研究棟III（C3棟）　3階　b3n03室（航空宇宙工学専攻会議室）
講演： Lagrangian Particle Simulations of Fluid Vortices
Prof. Robert Krasny
(Department of Mathematics, University of Michigan, USA)
要旨： We review some recent Lagrangian particle simulations of fluid vortices. Two examples are discussed, (1) vortex ring instability in 3D flow, and (2) vortex dynamics on a rotating sphere. These simulations use the Biot-Savart integral to recover the velocity from the vorticity, adaptive particle discretizations, and a tree code to reduce the CPU time from $O(N^2)$ to $O(N\log N)$, where $N$ is the number of particles.

分科会「非平衡現象の流体力学」（第7回）

平成26年度第7回講演会（日本航空宇宙学会関西支部分科会）

日時： 平成26年9月10日（水）　16:30-17:30
場所： 京都大学 桂キャンパスCクラスタ総合研究棟III（C3棟）　3階　b3n03室（航空宇宙工学専攻会議室）
講演： An immersed boundary method for Navier-Stokes equations on unstructured anisotropic meshes
Dr. Cécile Dobrzynski
(Institut Mathématiques de Bordeaux, Université Bordeaux 1, France)
要旨： Immersed boundary methods such as penalization present advantages in computational fluid dynamics.They simplify mesh generation and are widely used for moving bodies. However, an issue remains : the treatment of wall boundary conditions. Therefore mesh adaptation can be performed to improve the accuracy of wall treatments. In this work, we propose to solve the penalized Navier-Stokes equations with a residual distribution scheme combined with mesh adaptation. In addition, different ways of tracking an interface are presented to investigate unsteady problems dealing with moving bodies.

分科会「非平衡現象の流体力学」（第6回）

平成26年度第6回講演会（日本航空宇宙学会関西支部分科会）

日時： 平成26年8月18日（月）　16:10-18:10
場所： 京都大学 桂キャンパスCクラスタ総合研究棟III（C3棟）　3階　b3n03室（航空宇宙工学専攻会議室）
講演1： Regularity of Boltzmann Equation in Convex Domains
Prof. Yan Guo
(Division of Applied Mathematics, Brown University, USA)
要旨： It is known that discontinuity can be created at the boundary in a non-convex domain for the Boltzmann equation with initial and boundary conditions. In this talk, Boltzmann solutions are shown to be C^1 away from the grazing set of the phase boundary in a convex set.
講演2： Applications of finite volume analysis on UHVDC converter transformer design
Dr. Tor Laneryd
(ABB Corporate Research, Sweden)
要旨： Ultra-high voltage direct current (UHVDC) transformers allow large amounts of electricity to be transported across very long distances with minimal losses. Numerical analysis using finite volume schemes plays an important part in the design of UHVDC transformers, both for the cooling systems and for the electrical insulation. The former involves solving the well-known Navier-Stokes system of equations for mixed convection of the transformer oil that is characterized by its high Prandtl number. The latter is analyzed by a theoretical model of ion transport with governing equations dominated by the convection terms and requiring specialized boundary conditions on solid-liquid interfaces.